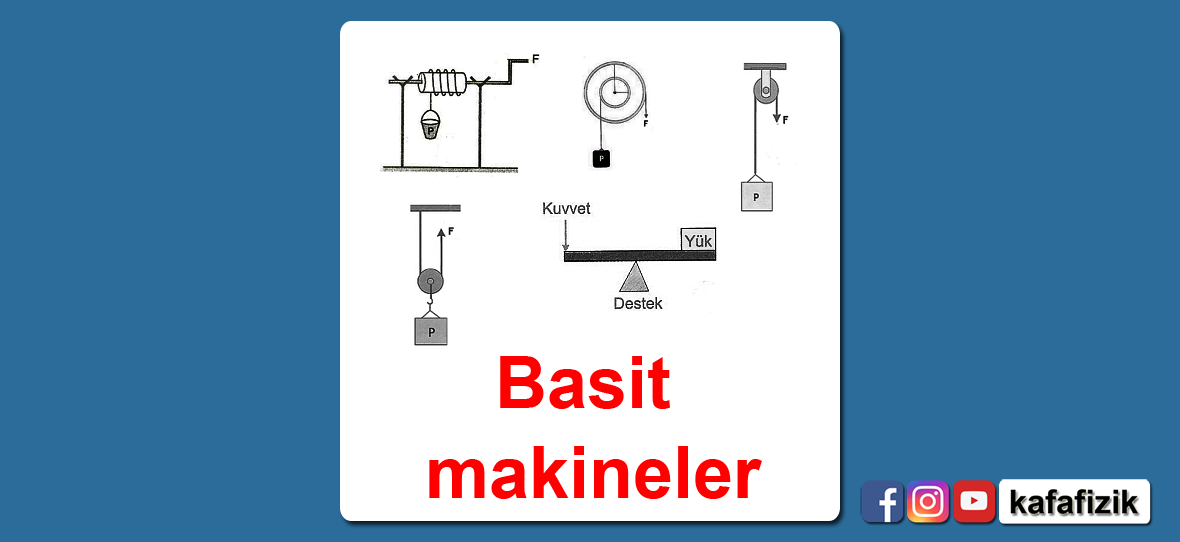
11.sınıf fizik dersi basit makineler konu anlatımı. Basit makinelerin özellikleri ve çeşitleri ders notları.
Basit makinelerin özellikleri
1- İş yapma kolaylığı sağlar
2- Tork, denge ve iş prensibine göre çalışırlar.
3- Kuvvetten veya yoldan kazanç sağlanır.
4- Kuvvetten kazanç varsa yoldan kayıp, kuvvetten kayıp varsa yoldan kazanç vardır.
5- İşten veya enerjiden kazanç sağlamaz.
Basit makineler kaldıraç, makara, eğik düzlem, vida, çıkrık ve dişli sistemlerini inceliyoruz.
Makaralar
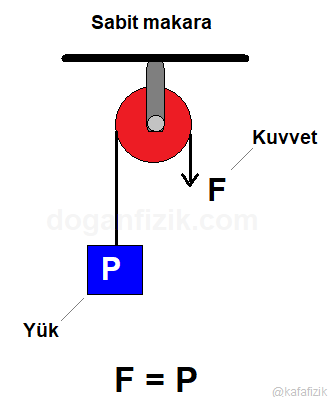
1- Sabit makara
Yükle beraber hareket etmeyen makaralara sabit makara denir.
Kuvvetten kazanç veya kayıp yoktur.
Amaç kuvvetin yönünü değiştirmektir.
F = P
İp 1 metre aşağı çekildiğinde yük de 1 metre yer değiştirir.
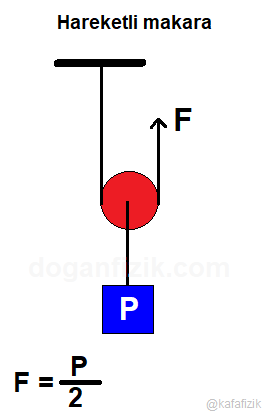
2- Hareketli makara
Yükle beraber hareket eden makaralara hareketli makara denir.
İpin bir ucu duvara bağlanmıştır, diğer ucuna ise kuvvet uygulanır.
Kuvvetten 2 katı kazanç ve yoldan 2 katı kayıp vardır.
Yükü 1 metre yer değiştirmek için ip 2 metre çekilmelidir.
P = 2F
Kaldıraçlar
Bir destek noktası etrafında dönebilen sisteme kaldıraç denir.
Kaldıraçlar yük, destek noktası ve kuvvetten oluşur.
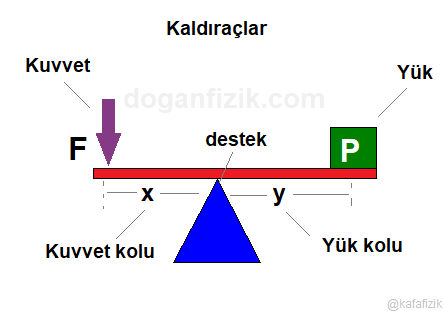
– Destek noktası : Kaldıracın etrafında döndüğü sabit noktadır.
– Kuvvet kolu : Kuvvetin destek noktasına olan uzaklığıdır.
– Yük kolu : Yükün destek noktasına olan uzaklığıdır.
Kaldıraç sorularını çözerken aşağıdaki tork eşitliğini kullanılırız.
Kuvvet.Kuvvet kolu = Yük.Yük kolu
F.x = P.y
Günlük hayatta pek çok kaldıraç türü basit makine kullanılır.
Kaldıraçlar desteğin, yükün ve kuvvetin bulunduğu yere göre üç çeşittir.
1- Desteğin ortada olduğu kaldıraçlar
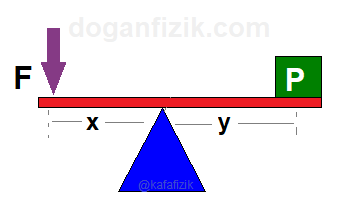
Örnekler: Kerpeten, makas, tahterevalli

2- Yükün ortada olduğu kaldıraçlar
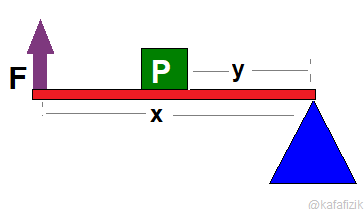
Örnekler: El arabası, ceviz kıracağı, menteşeli kapı, delgeç ve kapı kolu
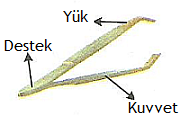
3- Kuvvetin ortada olduğu kaldıraçlar.
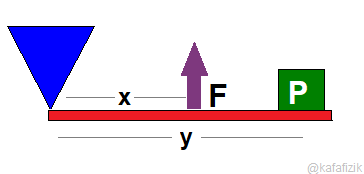
Örnekler: Cımbız, maşa, kürek ve tenis raketi
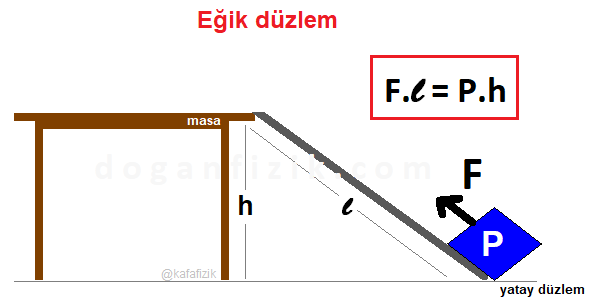
Eğik düzlem
Yükleri belirli bir yüksekliğe çıkarmak için tasarlanmış basit makinelere eğik düzlem denir.
Aşağıdaki görselde P yükü masa üzerine çıkarılmak isteniyor. P yükünü eğik düzlem kullanmadan masa üzerine çıkarmak istediğimizde yükün ağırlığı kadar kuvvet uygulamamız gerekir.
Yükü eğik düzlem kullanarak masa üzerine çıkarırsak kuvvetten kazanç sağlarız. Yük daha fazla yol alır (l>h) ancak daha az kuvvet uygulamış oluruz. (F>P). Eğik düzlem her zaman kuvvet kazancıyla iş kolaylığı sağlar.
F = kuvvet, ı = kuvvet kolu, p = yük ve h = yük kol olmak üzere F.l =P.h eşitliği ile sorular çözülür.
Örnek: Dağ yolları araçların yüksek kesimlere kolay bir şekilde çıkması için virajlı yapılır. Alınan yol uzar ancak, araçların dağa çıkışı kolaylaşır.
Vida
Vida kuvvet kazancı ile iş kolaylığı sağlar.
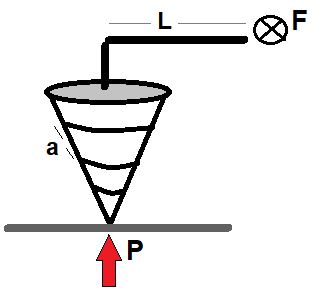
Vida üzerinde adım denilen girinti çıkıntılar bulunur. Adım miktarı (a) iki çıkıntı arası uzaklıktır.
F = Uygulanan kuvvet
2π.L = Kuvvetin aldığı yol (çevre)
P = Zemine uygulanan kuvvet veya tepki kuvveti
a = adım miktarı olmak üzere vida için eşitlik;
F.2π.L = P.a
şekilde yazılır.
h = Vidanın ilerleme miktarı
N = Tur sayısı olmak üzere
vidanın zeminde ilerleme miktarını veren formül;
h = a.N
Vidanın ilerleme miktarı sadece adım miktarı (a) ile tur sayısına (N) bağlıdır.
Çıkrık
İki silindir veya bir silindir ve bir koldan oluşan sistemlere çıkrık denir.
Örnek: Bisiklet pedalı, anahtar , el mikseri, araba direksiyonu
Dişli ve kasnaklar
Dişliler birbirine temas eder şekilde veya zincirle bağlıdır.
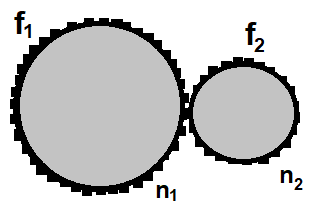
Tur sayıları dişli sayıları ile ters orantılıdır.
Birbirine temas eden dişliler zıt yönde dönerler.
f = tur sayısı ve n = dişli sayısı olmak üzere;
f1.n1 = f2.n2
eşitliğinden tur sayıları bulunur.
Kasnaklar
Kasnaklar birbirine kayışla bağlanmıştır.
Tur sayıları yarıçapları ile ters orantılıdır.
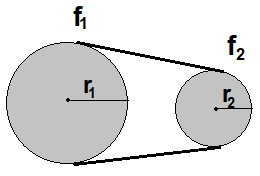
f = tur sayısı ve r = kasnak yarıçapı olmak üzere;
f1.r1 = f2.r2
eşitliğinden tur sayıları bulunur.
Perçinlenmiş kasnak ve dişliler
Birbirine merkezlerinden yapışık dişli ve kasnaklardır.
Aynı anda dönüş yaparlar.
Dönüş yönleri ve tur sayıları eşittir.
Aşağıdaki şekilde K ve L kasnakları perçinlenmiştir.
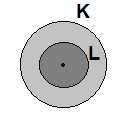
K ve L kasnakları aynı yönde, eşit tur sayısına sahiptir.
Dişli ve kasnakların dönüş yönleri
Kayışın düz veya ters bağlanmasına göre kasnakların dönüş yönleri değişir.
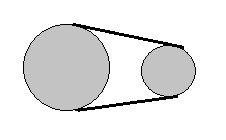
Düz bağlanmış kasnaklar aynı yönde dönerler.
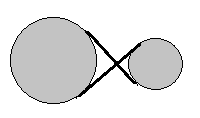
Zıt bağlanmış kasnaklar zıt yönde dönerler.